This IGCSE mathematics problem involves several core concepts and solution methods that must be well understood:
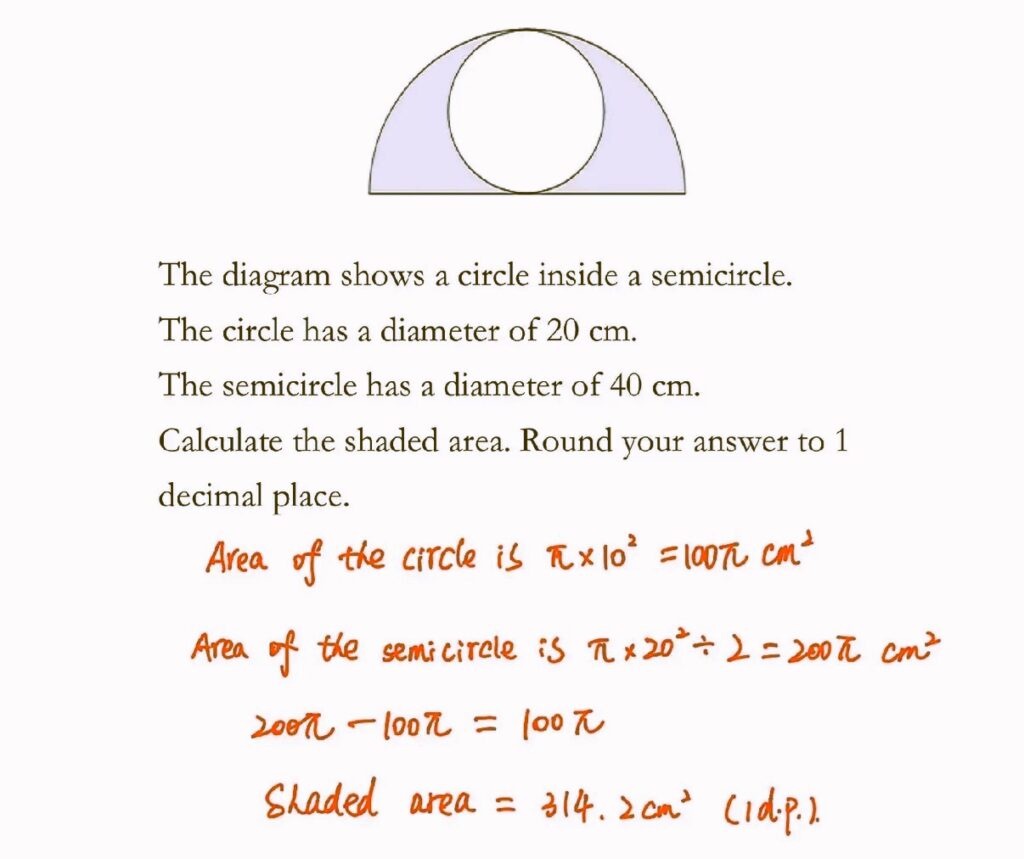
- Application of the circle area formula:
Using the formula for the area of a circle to calculate the areas of the small circle and the semicircle separately. This forms the core basis for finding the shaded area. - Calculation of the area of a semicircle:
The area of a semicircle is half of the area of the corresponding full circle. Students must understand the relationship between the areas of a semicircle and a full circle. - Finding shaded area using the subtraction (cut-and-fill) method:
Subtract the area of the inner small circle from the area of the semicircle to obtain the shaded region. This requires mastery of the “whole minus part” approach in solving geometric area problems. - Rounding decimal values:
According to the question’s requirement, the final result should be rounded to 1 decimal place. Students must be familiar with the rules of rounding decimal numbers.
Problems of this type require first calculating the areas of the circle and semicircle using the appropriate formulas, then applying the “total area minus empty area” method to find the shaded region, and finally rounding the answer as required. By combining circle area formulas with geometric subtraction techniques, the correct solution can be obtained.